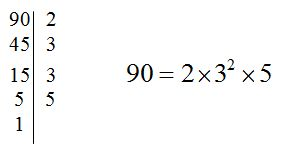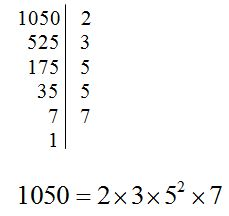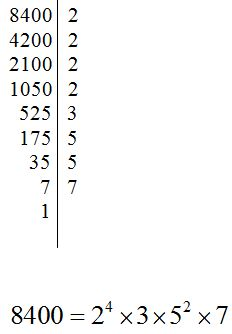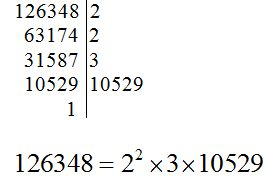Números primos y compuestos
- Un número primo se puede dividir exactamente sólo entre 1 y él mismo.
- Un número compuesto se puede dividir exactamente entre otros números además de 1 y él mismo.
- (Así que cualquier número entero mayor que 1 es primo o compuesto)
Ejemplos
Número |
Se puede dividir |
¿Primo o |
1 |
(1 no es primo ni compuesto) |
|
2 |
1,2 |
Primo |
3 |
1,3 |
Primo |
4 |
1,2,4 |
Compuesto |
5 |
1,5 |
Primo |
6 |
1,2,3,6 |
Compuesto |
7 |
1,7 |
Primo |
8 |
1,2,4,8 |
Compuesto |
9 |
1,3,9 |
Compuesto |
10 |
1,2,5,10 |
Compuesto |
Puedes profundizar un poco más sobre este tema en el siguiente enlace: https://www.smartick.es/blog/index.php/numeros-primos-y-numeros-compuestos/
Mínimo común múltiplo (mcm)
- El número más pequeño (no cero) que es múltiplo de dos o más números.
- El nombre de mínimo común múltiplo está hecho de las partes mínimo, común y múltiplo:
¿Qué es un "múltiplo"?
Los múltiplos de un número son lo que tienes cuando lo multiplicas por otros números (si lo multiplicas por 1, 2, 3, 4,5, etc.) como en las tablas de multiplicar.
Aquí tienes ejemplos:
Los múltiplos de 3 son 3, 6, 9, 12, 15, 18, 21, etc... |
Los múltiplos de 12 son 12, 24, 36, 48, 60, 72, etc... |
¿Qué es un "múltiplo común"?
Si tienes dos (o más) números, y miras entre sus múltiplos y encuentras el mismo valor en las dos listas, esos son los múltiplos comunes a los dos números.
Por ejemplo, si escribes los múltiplos de dos números diferentes (digamos 4 y 5) los múltiplos comunes son los que están en las dos listas:
Los múltiplos de 4 son 4,8,12,16,20,24,28,32,36,40,44,... |
Los múltiplos de 5 son 5, 10, 15, 20, 25, 30, 35, 40, 45,50,... |
¿Ves que 20 y 40 aparecen en las dos listas? Entonces, los múltiplos comunes de 4 y 5 son: 20, 40 (y 60, 80, etc. también) |
¿Qué es el "mínimo común múltiplo"?
Es simplemente el más pequeño de los múltiplos comunes. En el ejemplo anterior, el menor de los múltiplos comunes es 20, así que el mínimo común múltiplo de 4 y 5 es 20.
DESCOMPONER UN NÚMERO EN FACTORES PRIMOS
Imagina que tienes el número 12 y queremos descomponer en factores primos: un factor puede ser 6 otro, 2 y ya tenemos que 12 = 2 x 6
Pero 6 no es un número primo porque 6 = 2 x 3
Cuando vamos a descomponer un número en factores primos, comenzamos siempre por los factores más pequeños.
Escribimos el número a descomponer y a su derecha trazamos una recta vertical y detrás de ésta, vamos colocando los factores primos comenzando por el menor.
Ahora tienes que recordar muy bien cuándo un número es divisible por 2, 3, 5, 7, 11, 13,…………….



Siempre que descompongas un número en sus factores primos el último valor que aparecerá será el 1.
La respuesta se presenta:
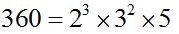
Como ves, se escribe el número y a su derecha en forma de producto (por eso estamos hablando de factores) los números primos con sus exponentes o número de veces que se repite cada factor.
Observa como hemos descompuesto los números: 90, 1050, 8400 y 126348:
|
|
|
|
A veces te pueden salir números primos muy grandes y es trabajoso comprobar que lo son.
Máximo común divisor
El máximo común divisor (m.c.d. o mcd) de dos o más números es el mayor número que divide a todos exactamente.
Cálculo del máximo común divisor
1 Se descomponen los números en factores primos.
2 Se toman los factores comunes con menor exponente.
3 Se multiplican dichos factores y el resultado obtenido es el mcd.
Ejemplo de cálculo de máximo común divisor
Hallar el m. c. d. de: 72, 108 y 60:
1 
Solución:
72 = 23 · 32
108 = 22 · 33
60 = 22 · 3 · 5
2 m. c. d. (72, 108, 60) = 22 · 3 = 12
12 es el mayor número que divide a 72, 108 y 60.
Caracteres de Divisibilidad
Evaluaremos algunas técnicas para conocer, por simple inspección, si un número es divisible por otro.
a) Divisibilidad por 2:
Un número es divisible por 2 cuando termina en cero o número par.
Ejemplo:
Podemos decir que 1184 es divisible por 2, ya que termina en número par.
b) Divisibilidad por 3:
Un número será divisible por 3 cuando la suma de sus dígitos nos dé múltiplo de 3.
Por ejemplo, tenemos 6345, entonces hacemos 6+3+4+5= 18, y como 18 es múltiplo de 3, concluimos que 6324 es divisible por 3.
c) Divisibilidad por 5:
Un número es divisible por 5 cuando termina en cero o cinco.
Por ejemplo, el número 530 es divisible por 5, ya que termina en 0.
Otro ejemplo sería el caso de 1995, número que también es divisible por 5, pues termina en 5.
d) Divisibilidad por 7:
En este caso lo mejor es ir directamente a un ejemplo:
Para saber si el número 2058 es divisible por 7, haremos lo siguiente |
|
Primero seleccionamos el ultimo digito y lo multiplicamos por 2 |
2058 x 2 = 16 |
Ahora el resultado lo restamos de la parte del número que no hemos utilizado, es decir, restamos 16 de 205. |
2058 x 2 = 16 |
Seleccionamos el último digito de lo que nos va quedando (de 189) y lo multiplicamos por 2 |
2058 x 2 = 16 |
El resultado lo restamos de la parte del número que no hemos utilizado, en este caso, restamos 18 de 18. |
2058 x 2 = 16 |
Si el residuo al final es cero (como en este caso) o múltiplo de siete, el número será divisible por 7. |
BIBLIOGRAFÍA – CIBERGRAFÍA
Números primos y compuestos, Recuperado en: http://www.disfrutalasmatematicas.com/numeros/primos-compuestos.html
Mínimo común múltiplo, Recuperado en: http://www.disfrutalasmatematicas.com/numeros/minimo-multiplo-comun.html
Descomponer un número en factores primos, Recuperado en: http://www.aulafacil.com/matematicas-divisibilidad/curso/Lecc-5.htm
Máximo común divisor, Recuperado en: http://www.vitutor.com/di/di/a_7.html
Caracteres de Divisibilidad, Recuperado en: http://rocky-marciano.lacoctelera.net/categoria/matematicas